Passive Aggressive の実装
『オンライン機械学習』を参考にして Passive Aggressive (PA) アルゴリズムを実装し、学習の様子を眺めてみます。PA の制約を緩めたアルゴリズムである PA-I, PA-II も実装し、これらの動作の違いについても実験を通して比較します。
www.kspub.co.jp
データの準備
前回の記事と同様に、Iris データセットを利用して二値分類を試します。scikit-learn を利用して Iris データセットを読み込んだ後、実験に適した形にデータを加工します。X の各列は "sepal length (cm)", "sepal width (cm)", バイアス項 (定数 1) を表します。y は "setosa" が正例 (+1), "versicolor" が負例 (-1) になります。
import numpy as np import pandas as pd from sklearn.datasets import load_iris iris = load_iris() df_all = pd.DataFrame(iris.data, columns=iris.feature_names) df_all['species'] = iris.target selected_species = [0, 1] selected_features = [0, 1] df = df_all[df_all['species'].isin(selected_species)] df = df.reindex(np.random.permutation(df.index)).reset_index(drop=True) X = df[selected_features].as_matrix() X = np.c_[X, np.ones(X.shape[0])] y = [1 if i == selected_species[0] else -1 for i in df['species']] n_samples, n_features = X.shape
特徴量の各次元の平均が 0 となるように平行移動しておきます。前回の記事では、学習データの半径を小さくすることでパーセプトロンの収束が速くなることを確認しました。
X[:, :-1] = X[:, :-1] - np.mean(X[:, :-1], axis=0)
ここまでの処理で得られたデータをグラフにプロットして確認します。
import matplotlib.pyplot as plt def plot_dataset(): pos_indices = [i for i in range(n_samples) if y[i] == 1] neg_indices = [i for i in range(n_samples) if y[i] == -1] plt.scatter(X[pos_indices, 0], X[pos_indices, 1], c='r', label=iris.target_names[selected_species[0]]) plt.scatter(X[neg_indices, 0], X[neg_indices, 1], c='b', label=iris.target_names[selected_species[1]]) plt.title('Iris dataset', fontsize=14) plt.xlabel(iris.feature_names[selected_features[0]], fontsize=11) plt.ylabel(iris.feature_names[selected_features[1]], fontsize=11) plt.legend() plot_dataset() plt.show()

PA による決定境界の学習
Passive Aggressive アルゴリズムを以下のように実装しました。後述する PA-I, PA-II で共通の実装を使えるように、重みベクトルの更新式を引数で受け取る形にしています。学習の過程を確認できるように、重みベクトル (w) が更新されるたびに反復回数 (t + 1), 正解数 (accuracy) と合わせて models に追加します。パーセプトロンでは、すべてのデータを正しく分類できた時点で反復計算を終了できましたが、PA では、すべての学習データのヒンジ損失が 0 になるまで計算を続けます*1。get_training_sample 関数は、学習データからランダムに 1 個のデータを選択する関数です。これは前回の記事で作成したものと同じです。
from random import randint def train_pa(update_fun, max_iter=100000): models = [] w = np.zeros(n_features) for t in range(max_iter): xt, yt = get_training_sample() if yt * w.dot(xt) <= 1: w = update_fun(w, xt, yt) accuracy = np.count_nonzero(y * X.dot(w) > 0) models.append({'t': t + 1, 'w': w, 'accuracy': accuracy}) if np.count_nonzero(y * X.dot(w) > 1) == n_samples: break return models def get_training_sample(): i = randint(0, n_samples - 1) return X[i, :], y[i]
def pa_update_fun(w, x, y): return w + hinge(w, x, y) / square_dist(x) * y * x def hinge(w, x, y): return max(0, 1 - y * w.dot(x)) def square_dist(x): return x.dot(x)
pa_update_fun 関数を train_pa に渡して、PA の学習を実行します。
models = train_pa(pa_update_fun)
学習結果として得られた決定境界をプロットします。models[-1]['w'] に最後の重みベクトルが格納されています。このベクトルによる決定境界を描画します。中央の直線が決定境界です。両側の灰色の直線は、正例、負例のそれぞれでヒンジ損失が 0 になる点です。正例と負例の中間に決定境界が引かれている様子を確認できました。
def plot_decision_boundary(w): plot_dataset() xmin, xmax = plt.xlim() ymin, ymax = plt.ylim() grid_x, grid_y = np.meshgrid(np.linspace(xmin, xmax, 100), np.linspace(ymin, ymax, 100)) grid_z = w[0] * grid_x + w[1] * grid_y + w[2] plt.contour(grid_x, grid_y, grid_z, colors=['gray', 'black', 'gray'], levels=[-1, 0, 1]) plt.show() plot_decision_boundary(models[-1]['w'])

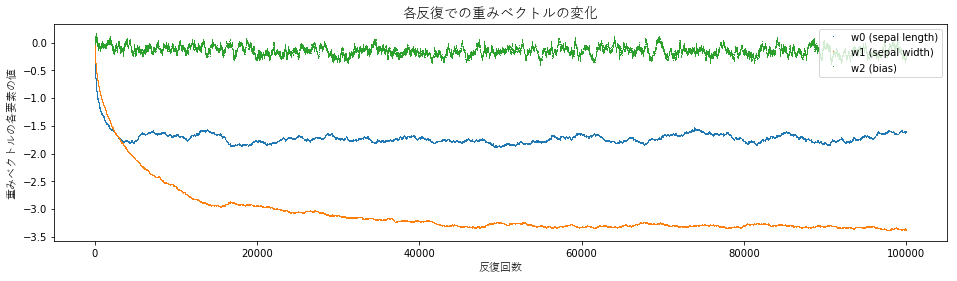
models の各要素をプロットして、学習の過程を詳細に見てみます。最初のグラフは、各反復での重みベクトルを決定境界としたときの正解数です。次のグラフは、各反復での重みベクトルの要素の値です。二つのグラフを比較すると、正解数が 100 になった後も重みベクトルの更新が続いている様子が分かります。
def plot_accuracies(models): ts = [m['t'] for m in models] accuracies = [m['accuracy'] for m in models] plt.figure(figsize=(16, 4)) plt.plot(ts, accuracies, marker=',', linestyle='None') plt.title(u'各反復での重みベクトルによる正解数の変化', fontproperties=fp14) plt.xlabel(u'反復回数', fontproperties=fp11) plt.ylabel(u'正解数', fontproperties=fp11) plt.ylim(48, 102) plt.show() def plot_weights(models): ts = [m['t'] for m in models] w0 = [m['w'][0] for m in models] w1 = [m['w'][1] for m in models] w2 = [m['w'][2] for m in models] plt.figure(figsize=(16, 4)) plt.plot(ts, w0, marker=',', linestyle='None', label='w0 (sepal length)') plt.plot(ts, w1, marker=',', linestyle='None', label='w1 (sepal width)') plt.plot(ts, w2, marker=',', linestyle='None', label='w2 (bias)') plt.title(u'各反復での重みベクトルの変化', fontproperties=fp14) plt.xlabel(u'反復回数', fontproperties=fp11) plt.ylabel(u'重みベクトルの各要素の値', fontproperties=fp11) plt.legend(loc='upper right') plt.show() plot_accuracies(models) plot_weights(models)


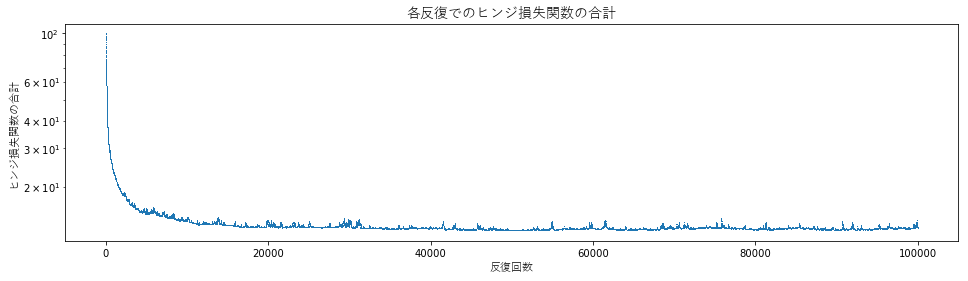
次に、各反復での重みベクトルによるヒンジ損失関数の合計値を確認します。この値が 0 になれば、PA はそれ以上重みベクトルを更新しないので、反復計算を終了できます。しかし、この実験では、反復計算が進むにつれて値が小さくなっていくものの、厳密に 0 にはならずに小さな値が残っています。
def calc_hinge_loss(w): return np.sum([1 - z for z in y * X.dot(w) if z < 1]) def plot_hinge_loss(models): ts = [m['t'] for m in models] losses = [calc_hinge_loss(m['w']) for m in models] plt.figure(figsize=(16, 4)) plt.plot(ts, losses, marker=',', linestyle='None') plt.title(u'各反復でのヒンジ損失関数の合計', fontproperties=fp14) plt.xlabel(u'反復回数', fontproperties=fp11) plt.ylabel(u'ヒンジ損失関数の合計', fontproperties=fp11) plt.yscale('log') plt.show() plot_hinge_loss(models)

線形分離不可能なデータへの適用
ここからは、線形分離不可能なデータに PA を適用して、どのような結果が得られるかを確認してみます。学習用データとして、Iris データセットの "versicolor" と "virginica" を利用します。この記事の冒頭のコードを、selected_species と selected_features を次のように変更して再実行します。
selected_species = [1, 2] selected_features = [2, 3]
得られる学習データは以下のとおりです。ちょうどよい具合に正例と負例が重なっています。

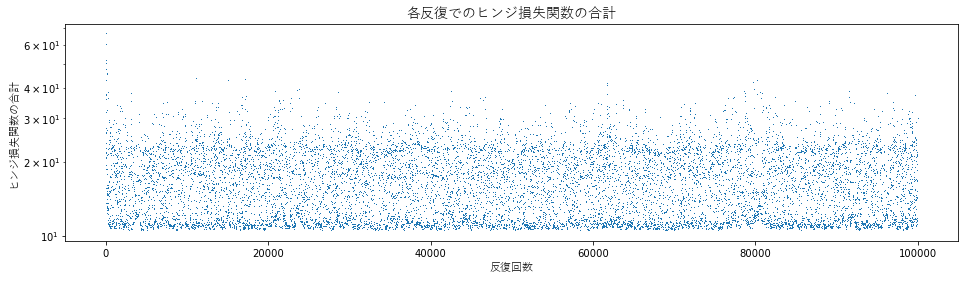
この学習データに PA を適用した結果を以下に示します。決定境界が versicolor 側に寄っていますが、そうならない場合もあります。反復ごとの正解数を見てみると、90 から 96 あたりを中心に変化し続けています*3。PA は各反復で与えられる一つの学習データについてヒンジ損失が 0 になるように重みベクトルを更新するので、線形分離不可能なデータでは収束しません。グラフからも、反復ごとに重みベクトルやヒンジ損失が大きく変動し続ける様子が分かります。



PA-I, PA-II による決定境界の学習
次に、PA 制約条件を緩めたアルゴリズムである PA-I, PA-II を実装して、このデータに適用します。PA, PA-I, PA-II の違いは重みベクトルの更新式だけなので、先ほど実装した pa_update_fun を差し替えることで簡単に実装できます。
PA-I の更新式の実装は以下のとおりです*4。PA-I ではコストが超パラメータとなります。pa1_update_fun は cost を受け取って実際の更新式 _pa1_update_fun を返す高階関数の形になっています。
def pa1_update_fun(cost): def _pa1_update_fun(w, x, y): return w + min(cost, hinge(w, x, y) / square_dist(x)) * y * x return _pa1_update_fun
PA-I は以下のように実行できます。実行例ではコストを 0.01 としました。pa1_update_fun(0.01) で得られた更新式を train_pa に渡して学習を行います。学習結果は、まずまず妥当な決定境界が得られているように見えます。また、反復ごとの推移を見てみると、PA の場合とは異なり、比較的なめらかに動いている様子が分かります。
models = train_pa(pa1_update_fun(0.01))




同様に PA-II でも確認します。PA-II の更新式の実装は以下のとおりです*5。
def pa2_update_fun(c): def _pa2_update_fun(w, x, y): return w + hinge(w, x, y) / (square_dist(x) + 0.5 / c) * y * x return _pa2_update_fun
こちらもコストを 0.01 として実行した結果を示します。PA-I の結果と似ていますが、重みベクトルの動き方はこちらの方が大きいようにも見えます。PA-I, PA-II とも、線形分離できないデータについて上手く動作している様子を確認できました。
models = train_pa(pa2_update_fun(0.01))