SVM による MNIST 手書き数字分類結果の詳細
LIBSVM の svm-train, svm-predict に -b 1 を指定すると、分類結果に加えて、データが各クラスに属する確率を出力してくれます*1。今回は、このオプションを指定して MNIST の手書き数字データを分類して、その結果を詳細に見てみたいと思います。
実行方法は前回と同様です。svm-train だけではなく svm-predict にも -b 1 を指定することに注意してください。その他のパラメータは前回求めた値を利用し、train.svm 全体を利用して学習しました。
$ libsvm-3.18/svm-train -c 1.41421356237 -g 0.03125 -b 1 train.svm train.model $ libsvm-3.18/svm-predict -b 1 t10k.svm train.model t10k.out Accuracy = 98.55% (9855/10000) (classification)
前回の実験では、train.svm 全体を利用した場合の正解率は 98.45% でしたが、今回は 98.55% と、前回よりも少し良い結果が得られました。
svm-predict に -b 1 を指定して実行すると、以下のような出力が得られます。先頭行はヘッダで、2 行目からが各データの分類結果です。データ行の各行は、1 列目が分類結果、2 列目以降が各クラスに属する確率です。各列がどのクラスに対応するかは、ヘッダ行に対応しています。昇順ではないことに注意してください*2。
$ head -n 5 t10k.out labels 5 0 4 1 9 2 3 6 7 8 7 8.45838e-09 8.5701e-09 7.2197e-09 4.36086e-09 2.06016e-08 1.20222e-08 3.11083e-08 3.84965e-09 0.999999 1.35788e-06 2 1.63721e-05 1.29293e-05 1.54913e-05 0.000207107 3.40861e-05 0.999285 0.000226826 2.96558e-05 6.90256e-05 0.000103885 1 4.96783e-06 3.5933e-06 0.000214841 0.999229 9.59665e-06 5.00089e-05 1.30477e-05 6.62649e-06 0.000320828 0.000147074 0 4.29045e-08 0.999928 2.4236e-06 3.41474e-05 1.13877e-05 4.42743e-06 1.20789e-06 1.14256e-05 5.92955e-06 8.05161e-07
各データについて、確率が最大になるクラスが分類結果となります。たとえば先頭行の分類結果は "7" ですが、この確率は 0.999999 と非常に大きな値になっています。一方、2 行目の分類結果は "2" で、その確率は 0.999285 となっています。
分類対象データ 10,000 件について、確率値がどのような分布になっているのかを確認してみます。まず、svm-predict で得られた t10k.out ファイルを正解ラベルと突き合わせて、csv 形式に整形します。以下のように書いてみました。
$ paste -d' ' \
<(cut -f1 -d' ' t10k.svm) \
<(tail -n +2 t10k.out |\
awk '{ imax = 2; for (i = 3; i <= NF; i++) if ($imax < $i) imax = i; print $1, $imax; }') |\
cat -n |\
sed 's/^ *//' |\
tr '\t ' ',' >results.csv出力される results.csv は以下のようになります。各行は、先頭から順に、データ番号 (t10k データセットでの出現順序)、正解 (手書きの数字)、分類結果、確率値を表します。
$ head -n 5 results.csv 1,7,7,0.999999 2,2,2,0.999285 3,1,1,0.999229 4,0,0,0.999928 5,4,4,0.999278
確率値のヒストグラムを表示させてみます。刻み幅は 0.01 (1%) としました。端数は切り捨てているので、100 の区画には確率値 1 のデータのみが含まれます。10,000 件中 8,707 件が 99% 以上の確率値で分類されていることが見て取れます。
$ awk -F, '{ print int($4 * 100) }' results.csv | sort -n | uniq -c | column
1 25 8 45 7 59 7 73 15 87
1 27 3 46 4 60 9 74 25 88
3 30 3 47 6 61 8 75 19 89
1 31 6 48 9 62 10 76 32 90
3 32 7 49 4 63 5 77 28 91
2 33 5 50 11 64 12 78 33 92
2 34 4 51 7 65 10 79 43 93
2 35 7 52 5 66 9 80 69 94
2 36 7 53 2 67 14 81 72 95
1 37 9 54 9 68 14 82 92 96
1 38 4 55 8 69 11 83 162 97
5 40 3 56 7 70 14 84 337 98
5 41 4 57 14 71 15 85 8079 99
1 43 8 58 9 72 18 86 628 100次に、これを累積度数分布の形にしてグラフに描画してみます。以下のようにデータをソートして、cat -n で順位をつけておきます。
$ sort -t, -nsk4 results.csv | cat -n | tr -d ' ' | tr '\t' ',' >results_sorted.csv
先ほどのヒストグラムで、10,000 件中 8,707 件が 99% 以上でしたので、確率の昇順にソートすると、先頭の 1,293 行が 99% 未満、1,294 行目で 99% 以上になっているはずです。検算として、このことを確認します。
$ tail -n +$((10000 - 8707)) results_sorted.csv | head -n 2 1293,6745,2,2,0.98999 1294,7477,3,3,0.990034
また、正しく分類できなかったデータを以下のようにして抽出しておきます。
$ awk -F, '$3 != $4' results_sorted.csv >incorrect.csv
抽出結果はこのようになります。第 3 列が実際に書かれた数字、第 4 列が SVM による判別結果です。
$ head -n 5 incorrect.csv 1,4164,9,0,0.256061 3,2608,7,2,0.304143 5,660,2,8,0.30977 6,6626,8,4,0.311811 7,1040,7,9,0.322256
これらをグラフにしたものが次の結果です。横軸が確率値、縦軸が累積のデータ数です。オレンジ色の各点は、正しく分類できなかったデータを示しています。このようにグラフに表してみると、データ全体の中でも確率の低い方に誤りが集中していることが分かります。

さて、前々回の記事で、MNIST の手書き数字データを画像ファイルに変換する手順を紹介しました。これを利用して、正しく分類できなかった数字がどのようなものか、画像を確認してみます。
比較のため、まずは正しく分類できた数字の画像を見てみます。とはいえ、ほとんどの画像は正しく分類できているので、すべてを列挙するわけにはいきません。ここでは、0 から 9 の各数字について、確率の高かったものを 10 個ずつ選択しました。結果は以下のようになりました。
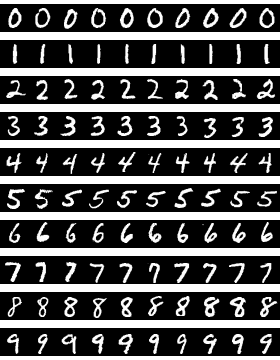
これに対して、正しく分類できなかった 145 文字は以下のとおりです。こうしてみると、やはり、人が見ても判別しにくい汚い文字で分類に失敗していると言えそうです。
